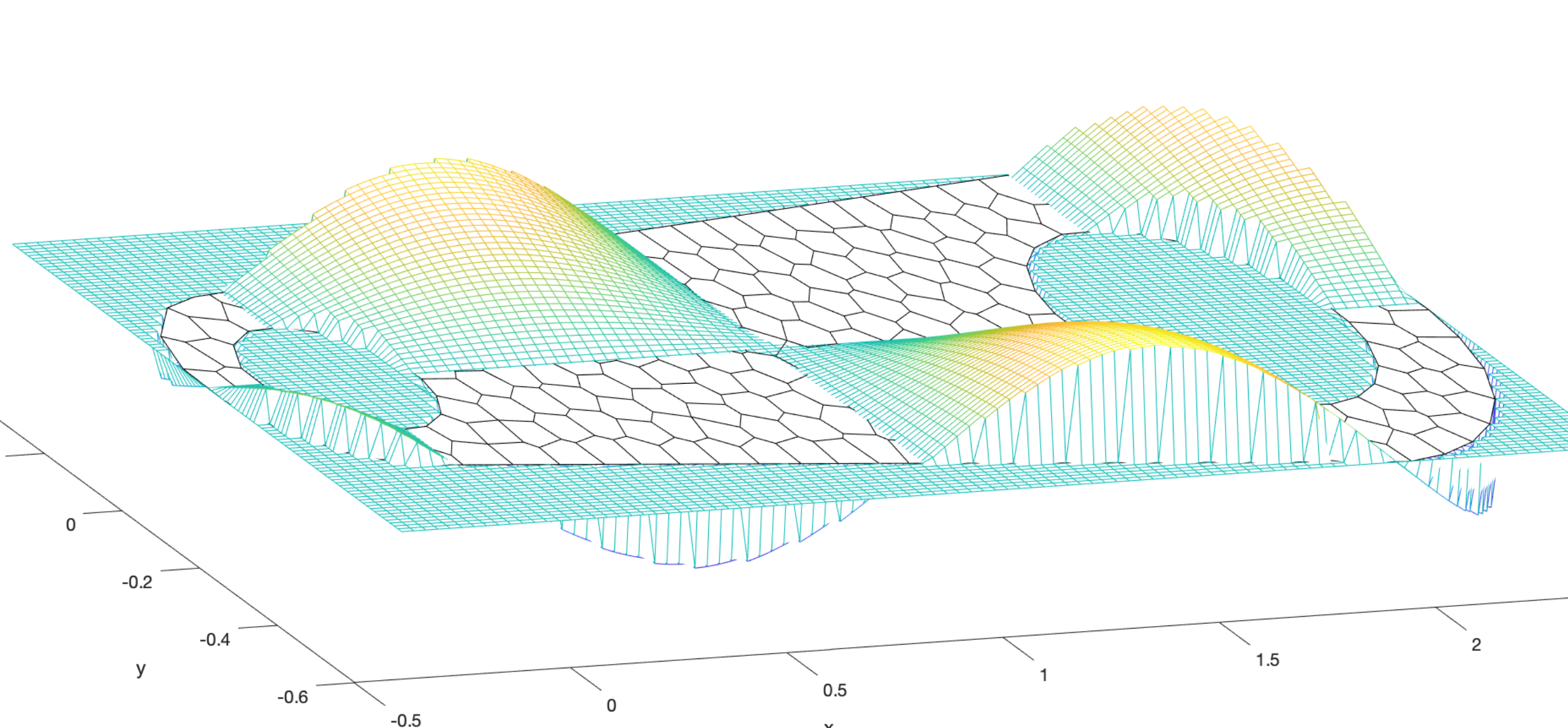
The study of algorithms for numerical approximation

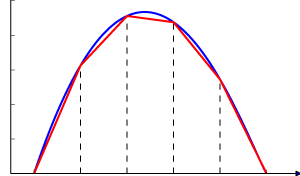
Finite element methods. The aim is to solve all kinds of PDEs efficiently and to within specified error bounds using unstructured, polyhedral, and refined computational meshes.

Discontinuous Galerkin (DG) and Discontinuous Petrov Galerkin (DPG) methods. These are special finite element methods, and the goal is to understand and exploit their many advantageous properties.

Isogeometric analysis. The vision is an integration of computational geometry and analysis, by unifying the disparate methods and data structures of Computer Aided Geometric Design (CAGD) and finite element analysis.

Approximation of div-curl PDE systems. These arise in many problems of mechanics and physics, such as those involving electromagnetism, acoustics, and diffusion. They have a precise mathematical structure, and the challenge is to preserve this structure within the numerical methods.

Fluid structure interaction (FSI) problems. These arise in many important applications, and involve complex numerical issues related to mechanical structures deforming within a fluid.

Hyperbolic conservation laws. These PDEs model, e.g., transport processes, fluid dynamics, and turbulence. The equations offer special challenges related to the interaction of numerics and physics, such as arise in the formation of shocks and dealing with nonuniqueness of solutions.

Boltzmann type equations and particle transport. Challenges include preservation of physics in numerical methods at quantum, kinetic, and fluid scales, and approximation of high-dimensional non-equilibrium statistical flows.

Multiphysics simulation. A complex system often contains many smaller, coupled subsystems. Solving them iteratively leads to possible nonconvergence of the overall problem and issues of propagation of errors between subsystems.

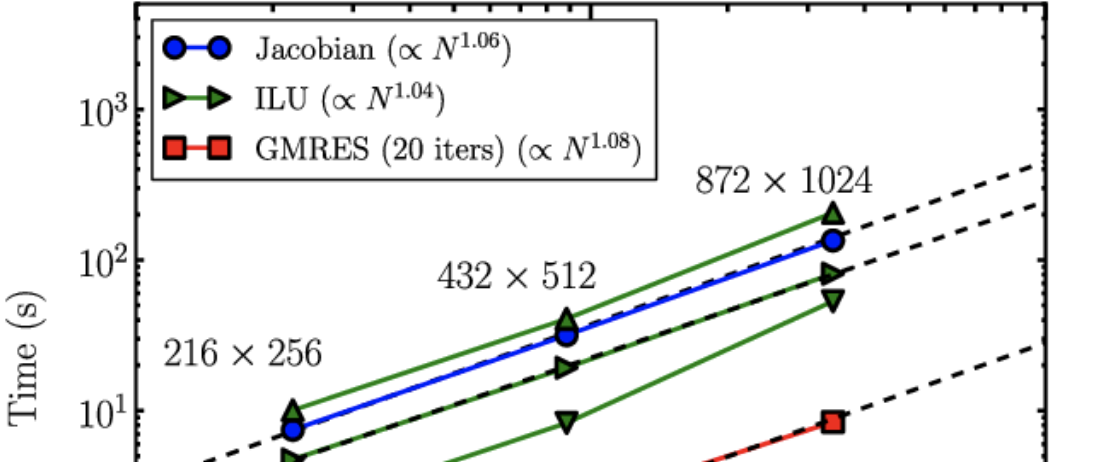
Solution of linear systems. Most numerical methods reduce at some level to very large systems of linear equations, and the overall computational cost is related most strongly to the time needed to solve these linear systems. Algorithms using direct, probabilistic, and iterative methods are explored in a massively parallel, high performance computational setting.